Die gleichstufige Stimmung - Was ist das?
Zur Erläuterung der gleichstufigen Stimmung muß ich etwas weiter ausholen. Stellen wir uns daher zunächst eine einfache Versuchsanordnung vor. Durch ein Gewicht wird eine Saite gespannt und deren Abschnitt zwischen den beiden Stegen wird zum Schwingen angeregt. Bei einer Saitenlänge L0 wird so ein Ton mit der Frequenz f0 erzeugt.

Wenn wir nun die Länge der Saite halbieren, wird die Schwingung der Saite dadurch doppelt so schnell. Es ergibt sich daraus folgende einfache Beziehung: Wenn L = L0 / 2 ist, dann wird f = 2 * f0 . Frequenz und Länge verhalten sich somit umgekehrt proportional zueinander. Je kürzer die Länge L wird, umso größer wird die Frequenz f.
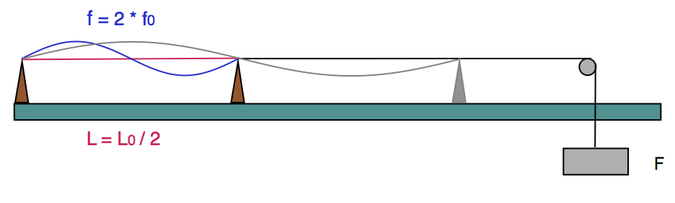
Musikalisch betrachtet entspricht das Verhältnis f / f0 = 2 genau dem Intervall einer reinen Oktave aufwärts. Pro Oktave aufwärts verdoppelt sich jeweils die Frequenz und pro Oktave abwärts halbiert sie sich.
Allgemein gilt daher: f = f0 * 2n ,wobei n = 1, 2, 3, 4 ... für die Anzahl der Oktaven aufwärts von f0 und n = -1, -2, -3 ... für die Anzahl der Oktaven abwärts von f0 ist.

Wird die Saitenlänge auf 2/3 der ursprünglichen Länge gekürzt, so verändert sich die Frequenz wiederum genau umgekehrt und wird daher um den Faktor 3/2 größer. Musikalisch gesehen entsteht so das Intervall einer reinen Quinte aufwärts. Würde man die verbleibende Länge erneut auf 2/3 kürzen, so würde sich die Frequenz nochmals um den Faktor 3/2 erhöhen.
Für die Quinten gilt also: f = f0 * (3/2)m ,wobei m = 1, 2, 3, 4 ... für die Anzahl der Quinten aufwärts von f0 und m = -1, -2, -3 ... für die Anzahl der Quinten abwärts von f0 ist.
Die Intervalle in der Partialtonreihe

Anhand der Partialtonreihe kann man durch Vergleich der Teiltöne die Zahlenverhältnisse der reinen Intervalle sehr einfach ablesen. Zum Beispiel hat das Oktavintervall vom 2. zum 1. Teilton das Frequenzverhältnis 2:1 bzw. die Oktave vom 4. zum 2. Teilton das Verhältnis 4:2, was gekürzt wiederum 2:1 ergibt.
Die Quinte ergibt sich vom 3. zum 2. Partialton mit dem Verhältnis 3:2. Die Quarte liegt zwischen dem 4. und dem 3. Partialton und hat das Verhältnis 4:3. Des Weiteren sieht man noch die große Terz 5:4 oder weiter oben in der Reihe 10:8 (=5:4), die kleine Terz 6:5 oder weiter oben 12:10 (=6:5), die große Sexte 5:3 sowie die kleine Sexte 8:5.
Bemerkenswert ist aber, dass es in der Naturtonreihe zwei unterschiedliche Ganztonschritte gibt, nämlich 9:8 und 10:9. Deswegen gibt es auch zwei verschiedene kleine Septimen 9:5 und 16:9. Darüber hinaus gibt es noch die Naturseptime 7:4, die aber zu eng ist, weil der 7. Teilton im Vergleich zum notierten Ton zu tief ist.
Konsonanz von Zweiklängen
Besonders wohlklingend oder konsonant empfinden wir unter den Zweiklängen die Oktave (2:1), bei welcher der höhere Ton exakt die doppelte Frequenz des tieferen Tons hat. Die Phasenbeziehung zwischen den beiden Tönen ist dabei entscheidend für unser Empfinden von Konsonanz.
Je schneller die beteiligten Schwingungen wieder in der Anfangsphasenlage zueinander stehen, umso konsonanter werden sie wahrgenommen. Bei einer Oktave wird bereits nach zwei Schwingungen des oberen Tons und einer Schwingung des unteren Tons wieder die ursprüngliche Phase erreicht. Bei der Quinte (3:2), dem für uns zweitbesten konsonanten Zweiklang, stellt sich die Anfangsphase nach drei Schwingungen des oberen Tons und zwei Schwingungen des unteren Tons ein. Weitere Zweiklänge nach abnehmender Konsonanz geordnet sind die Quarte (4:3), die große Sexte (5:3), die große Terz (5:4), die kleine Terz (6:5) und die kleine Sexte (8:5).
Die Entwicklung eines Tonleitersystems
Schon in der Antike war man bestrebt, durch aufeinanderfolgende reine Quinten ein Tonleitersystem zu entwickeln, welches sich nach jeweils einer Oktave wiederholt. Dabei tritt aber leider eine grundlegende Schwierigkeit auf, denn es gibt kein Tonsystem, das auf lauter reinen Quinten aufgebaut ist und bei dem nach m-Quinten die Oktave zum Anfangston exakt erreicht wird. Eine weitere und nicht erfüllbare Forderung für das Tonleitersystem ist, dass die konsonanten Intervalle möglichst rein abgebildet werden.

Das Verhältnis des Faktors für die Quinten zum Faktor für die Oktaven müßte nämlich für m-Quinten und n-Oktaven genau 1 werden. Dies kann mathematisch aber nie der Fall sein, weil 3m nie gleich 2n werden kann.
Das Verfahren der Skalenentwickung über Quinten folgt einem einfachen Prinzip. Ausgehend von einem Grundton werden Quintschritte aufwärts durchgeführt (Frequenz * 1,5) und es entstehen dabei jeweils neue Töne. Überschreitet man den Oktavton, so wird von dem neuen Ton aus abwärts reoktaviert (Frequenz * 0,5), um immer in der gleichen Oktave zu bleiben. Die Skalenentwicklung endet, wenn man nach m-Quintensprüngen und n-Oktavsprüngen wieder beim Grundton ankommt.

In nebenstehender Tabelle sieht man, wo die 2er-Potenzen mit geringer Abweichung den 3er Potenzen gleichen. Dies ist z. B. bei 5 Quinten und 3 Reoktavierungen der Fall, 243 ist ungefähr gleich 256 oder anders ausgedrückt: 243 / 256 = 0,949212 ist ungefähr 1. Der Fehler beträgt -0,05078. Die nächste, allerdings schlechtere Näherung gibt es bei 7 Quinten und 4 Reoktavierungen. Hier ist das Verhältnis 2187 / 2048 = 1,06787 und der Fehler beträgt + 0,06787.
Bei 12 Quinten und 7 Reoktavierungen findet man eine weitere und deutlich bessere Näherung. Das Verhältnis ist hier 531441 / 524288 = 1,01364 (Phythagoreisches Komma) und der Fehler ist nur noch +0,01364. Das 12-Tonsystem bildet die Quinten und Quarten sehr gut und die übrigen konsonanten Intervalle hinreichend gut ab.
Eine weitere Verringerung des Fehlers ergibt sich rechnerisch erst bei 53 Quinten und 31 Reoktavierungen. Das Verhältnis der beiden Faktoren ergibt hier 1,00209 und der Fehler liegt somit bei nur noch +0,00209. Alle konsonanten Intervalle sind im komplexen 53-Tonsystem sehr gut, d.h. mit nur geringem Fehler abgebildet. Allerdings gibt es hier auch wesentlich mehr dissonante Intervalle als dies im 12-Tonsystem der Fall ist.
Ein System mit 53 Tönen pro Oktave ist im Übrigen für die musikalische Praxis zu komplex.

Wenn man nun im bevorzugten 12-Tonsystem die aufeinanderfolgenden, reinen Quinten anschaulich in einer Kreisform, dem Quintenzirkel darstellt, so schließt sich der Kreis leider nicht und wir erhalten dadurch eher eine Spirale. Das letzte Intervall von E# nach H# ist ein wenig zu weit und H# ist deswegen ungleich C.
Die Quinte vom E# zum H# wird deutlich dissonant empfunden und wegen Ihres schrecklichen Heulens auch "Wolfsquinte" genannt.
Die Wolfsquinte wurde bei historischen Stimmungen,
z. B. bei den mitteltönigen Stimmungen, zugunsten von relativ reinen großen Terzen in Kauf genommen.
Harmonische Progressionen über die zwölf Tonarten sind aber in solchen historischen Stimmungen nicht möglich, es gibt vielmehr bevorzugte Tonarten und solche, die musikalisch völlig unbrauchbar sind.

Das Verhältnis von 12 Quinten zu 7 Oktaven ergibt also nicht 1, sondern 1,01364... Diese Abweichung nennt man das Phythagoreische Komma. Ein Klavier mit Oktaven zu jeweils 12 Halbtönen läßt sich daher nicht mit reinen Quinten stimmen.
Die logarithmische Einheit cent
Um Frequenzabweichungen einfacher darstellen und berechnen zu können, wurde die logarithmische Einheit cent (abgekürzt ct) definiert. Statt Frequenzverhältnisse zu multiplizieren oder zu dividieren, kann man bei einer logarithmischer Darstellung einfach addieren bzw. subtrahieren.
Jeder Halbtonschritt in einem 12-Tonsystem wird seinerseits in 100 Schritte geteilt, wodurch sich für eine Oktave mit dem Frequenzverhältnis fv von 2:1 dann genau 1200 Schritte ergeben. Mathematisch ausgedrückt sieht das dann so aus:

Zur Umrechnung eines in ct angegebenen Intervalls kann man folgende Gleichung aufstellen, wobei fv das gesuchte dezimale Frequenzverhältnis und x das Intervall in ct ist :
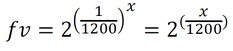
Die Umrechnung eines Frequenzverhältnisses fv in einen ct-Wert x lässt sich folgendermaßen durchführen:

Die gleichstufig temperierte Stimmung

Zur vollständigen Auflösung des phythagoreischen Kommas (PK) wird in der gleichstufig temperierten Stimmung das PK gleichmäßig auf alle 12 Quinten verteilt. Jede Quinte muss hierzu um die 12te Wurzel des PK, also um 1,00113 verringert werden.
Oder einfacher in ct umgerechnet:

Das PK ergibt in ct ausgedrückt eine Abweichung von 23,46 ct.

Die Abweichung der Quinten von der reinen Quinte beträgt 1,955 ct.

Die Quinten müssen also um den kleinen Betrag von 1,955 ct enger gestimmt werden, sind dadurch unrein oder temperiert und demzufolge nicht ganz schwebungsfrei.
Diese Abweichung ist aber so gering, dass unser Ohr diese Quinte dennoch als sehr rein empfindet.
Der Quintenzirkel schließt sich durch diese Maßnahme perfekt und die letzte Quinte vom E# zum H# klingt wie alle anderen Quinten vorher, da das H# jetzt die gleiche Tonhöhe wie das C hat. Es entsteht an keiner Stelle eine Wolfsquinte.
Die Quinte im gleichstufigen 12-Tonsystem besteht aus 7 Halbtonschritten zu je 100 ct und ergibt ein Intervall von 700 ct. Das Frequenzverhältnis fv berechnet sich zu:

und ist somit etwas kleiner als das Verhältnis 1,5 der reinen Quinte.
Die reine Quinte hat ein Frequenzverhältnis von 3:2 oder 1,5 und der ct-Wert x berechnet sich über:
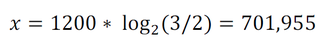
Die Quinte in der gleichstufigen Stimmung beträgt nur 700 ct und ist daher um 1,955 ct zu tief oder zu eng, wie der Klavierstimmer sagt.
